prueba sumativa : 10 CASO DE FACTORIZACION

PRUEBA SUMATIVA

Factoreo :

1°CASO FACTOR COMÚN:

Sacar el factor común es añadir la literal común de un polinomio, binomio o trinomio, con el menor exponente y el divisor común de sus coeficientes.
REGLA: Cuadrado del primer término más o menos cuadrado del segundo por el primero más cuadrado del segundo, y no hay que olvidar, que los dos que son positivos iguales funcionan como el primer término, sabiendo esto, será sumamente sencillo resolver los factores comunes.
EJERCICIOS:

4x + 4y= 4( x + y )
5a - 10b = 5(a - 2b)
2x + 6x = 2x( 1 + 3 )
3a - 6ab = 3a( 1 - 2b )

EJERCICIOS SIN RESOLVER:

3x + 9 :
5a + 5 :
4x + 8 :
4x + 8x :
x - 3x :
2x - x :
2x - 4x:
m - 2m
2x - 2x
4b + 4b

IMAGEN :

VIDEO:

2° CASO FACTOR COMÚN POR AGRUPACIÓN DE TÉRMINOS:

Consiste en agrupar entre paréntesis los términos que tienen factor común, separados los grupos por el signo del primer término de cada grupo. La agrupación puede hacerse generalmente de más de un modo con tal que los dos términos que se agrupen tengan algún factor común, y siempre que las cantidades que quedan dentro del paréntesis después de sacar el factor común en cada grupo, sean exactamente iguales. Después de lo anterior se utiliza el procedimiento del caso I, Factor Común.

EJERCICIOS:

* ax + bx + ay + by = ( ax + ay ) + (bx + by )

= x (a + b) +y ( a+b )

= (a + b ) (x + y )

* 3ax - 3x + 4y - 4ay = ( 3ax - 4ay ) - ( 3x - 4y )

= ( 3x - 4y ) - (3x - 4y )

= ( 3x - 4y )(a - 1 )

* 4a + 4b + xa + xb = 4 ( a + b ) + x ( a + b )

= ( a + b ) ( 4 + x )

* am - bm + an - bn = ( am + an ) ( - bm - bn )

= a ( m + n ) + b ( m - n )

( m + n ) ( a - b )

EJERCICIOS SIN RESOLVER :

ax - 2bx - 2ay + 2by =
6ax + 3a + 1 + 2x =
6m - 9n + 21nx - 14mx =
1 + a + 3ab + 3b =
20ax - 5bx - 2by + 8ay =
2am - 2an + 2a - m + n - 1 =
3ax - 2by - 2bx - 6a + 3ay + 4b =
ax - ay + az + x - y + z =
3x^3 - 9ax^2 + x + 3a =
3a - b^2 + 2b^2x - 6ax =

IMAGEN :

VÍDEOS:

3° CASO : TRINOMIO CUADRADO PERFECTO

Una cantidad es cuadrado perfecto cuando es el cuadrado de otra cantidad osea cuando es el producto de dos factores iguales.

REGLA:

Se extrae la raiz cuadrada al primero y tercer terminos del trinomio y se separan estas raices por el signo del segundo termino. el binomio asi formado, que es la raiz cuadrada del trinomio se multiplica por si mismo o se eleva al cuadrado.

EJERCICIOS:

* m^2 + 2m + 1 =

( m + 1 ) ( m + 1 ) = ( m+ 1 ) ^2

*4x^2 + 25y^2 - 20xy =

( 2x - 5y ) (2x - 5y ) = ( 2x - 5y ) ^2

* 1 - 16ax^2 + 64a^2x^4 =

(1 - 8ax^2) (1 - 8ax^2) = (1 - 8ax^2) ^2

* a^2 - 2ab + b^2 =

(a + b)(a + b)=(a + b)^2

EJERCICIOS SIN RESOLVER :

36 + 12m^2 + m^4 =
a^8 + 18a ^4 + 81 =
9b^2 - 30a^2b + 25a^4 =
a^2 - 10a + 25 =
16 + 40x^2 + 25x^4 =
1 + 14x^2y + 49x^4y^2 =
9 - 6x + x^2 =
a^6 - 2a^3b^3 + b^6 =
4x^2 - 12xy + 9y^2 =
1 + a^10 - 2a^5 =

IMAGEN :

VÍDEO:

4° CASO : DIFERENCIA DE CUADRADOS PERFECTOS

la suma de dos cantidades multiplicadas por su diferencia es igual al cuadrado del minuendo menos el cuadrado del sustraendo.

REGLA:

Se extrae la raíz cuadrada del minuendo y al sustraendo y se multiplica las suma de estas raíces cuadradas por la diferencia entre la raíz del minuendo y al del sustraendo

EJERCICIOS:

* 1 - a ^2 = ( 1 + a )(1 - a )

* 16x^2 - 25y^4 = (4x + 5y^2 )(4x - 5y^2)

*49x^2y^6z^10 - a^12 = ( 7xy^3z^5 + a^6) ( 7xy^3z^5 - a^6)

*x^2 - y^2 = ( x + y )(x - y )

EJERCICIOS SIN RESOLVER :

a^2 - 1 =
4a^4 - 9 =
100 - x^2y^6 =
16 - n^2 =
25x^2y^4 - 121 =
a^2m^4n^6 - 144=
256a^12 - 289b^4m^10 =
1 - 49a^2b^2 =
a^2 - 25 =
1 - 9^2b^4c^6d^8=

IMAGEN :

VÍDEO:

5°CASO: TRINOMIO CUADRADO PERFECTO POR ADICION Y SUSTRACION :

Se comprueba si el termino es cuadrado perfecto, si se extrae la raíz cuadrada del primero y tercero; las raíces cuadradas se multiplican por dos, si se le compara con el segundo termino tenemos un trinomio cuadrado perfecto

REGLA:

Se ordena el trinomio, se extrae ala raíz cuadrada del primer y del tercer termino, se halla el doble producto del las raíces de las anteriores, se compara el resultado con el segundo termino; se suma o se resta la cantidad necesaria para crear el segundo termino si es necesario y se suma o se resta la misma cantidad en el paso anterior para no alterar la expresión

EJERCICIOS:

*a^2 + 2a - 15 = ( a + 5 ) ( a - 3 )

* x^4 + x^2y^2 + y^4

+ x^2y^2 - x^2y^2

x^4+2x^2y^2 +y^4-x^2y^2 = ( x^4 + 2x^2y^2 + y^4 ) - x^2y^2

* 4a^2 + 8a^2b^2 + 9b^4

+ 4a^2b^2 - 4a^2b^2

4a^4 + 12a^2b^2 + 9b^2 - 4^2b^2 = ( 4a^4 + 12a^2b^2 + 9b^4) - 4a^2b^2

*a^2 - 16a^2b^2 + 36b^4

+4a^2b^2 - 4 a^2b^2

a^4 + 12a^2b^2 + 36b^4 - 4a^2b^2 =(a^4 + 12a^2b^2 + 36b^4 ) - 4a^2b^2

EJERCICIOS SIN RESOLVER :

a^4 + a^2 + 1 :
m^4 + m^2n^2 + n^4 :
x^8 + 3x^4 + 4
a^4 + 2a^2 + 9
a^4 - 3a^2b^2 + b^4
x^4 - 6x^2 + 1
4a^4 + 3a^2b^2 + 9b^4
4x^4 - 29 x^2 + 25
x^8 + 4x^4y^4 + 16y ^8
16m^4 - 25m^2n^2 +9n^4

IMAGEN:

VÍDEO:

6° CASO TRINOMIO DE LA FORMA X^2 + BX + C

a factorizar un trinomio de la forma x2+bx+c. entonces lo primero que debemos hacer es aprender a interpretar este tipo de trinomios. Hasta ahora hemos visto trinomios cuadrados perfectos que se asemejan con este en su condición especial. Primero es que el primer término que es x2 viene acompañado siempre y únicamente de uno positivo, si digamos tenemos un uno negativo entonces sacamos uno menos, cosa que nos cambie el signo del uno (el x2 puede variar de letra). Para resolver este tipo de trinomios el procedimiento es muy simple, hay que verificar si cumple la forma, se abren los paréntesis y tomamos la raíz del primer término. La raíz del primer término, con el signo que acompaña la b y el otro signo es la multiplicación de estos signos. Tenemos que encontrar un número que multiplicados den c y sumados o restados de b y esos dígitos se ponen entre los paréntesis al lado de la raíz del primer término. Hay que recordar que se debe verificar si es un trinomio de esa forma al reemplazar la fórmula en el trinomio. El primer signo siempre es el que acompaña a b y el signo siguiente es el que acompaña c por el que acompaña a b. Cuando c sea un número muy grande simplemente se descompone para poder encontrar y hacer las posibles combinaciones. Es muy importante como poner los dos números de la descomposición, siempre primero va el mayor, sino no nos queda bien la factorización. Primero va el mayor a la izquierda y el menor a la derecha.Asíi aprendimos a factorizar trinomios de la forma x2+bx+c.

REGLA:

Se escribe un paréntesis.

Se obtiene la raíz cuadrada del primer término.

Se obtiene la raíz cuadrada del tercer término y se escribe en el paréntesis.

El signo del binomio se toma del signo que tenga el segundo término del trinomio.

El binomio se eleva al cuadrado.

EJERCICIOS :

x^²-20xy+25y^²

2) 25x^²+30x+9

3) 3a^³+24a^²b+48ab^²

4) 100x^¹⁰-60c^⁴x^⁵y^⁶+9c^⁸y^¹²

5) 100x^⁶-160x^³y^³+64y^⁶

6) 9x^⁴-36x^²y^³+36y^⁶

7) 36y^²-48y+16

8) 4a^²-32a+64

9) 64x^⁴-64x^²+16

10) 81x^⁴y^⁴-72x^²y^²+16

Solución.

1) (2x-5y)^²

2) (5x+3)^²

3) 3a(a+4b)^²

4) (10x^⁵-3c^⁴y^⁶)^²

5) (10x^³-8y^³)^²

6) (3x^²-6y^³)^²

7) (6y-4)^²

8) (2a-8)^²

9) (8x^²-4)^²

10) (9x^²y^²-4)^²

EJERCICIOS SIN RESOLVER :

x^2 + 7x + 10
x^2 - 5x + 6
x^2 + 3x - 10
x^2 + x - 2
a^2 + 4a + 3
m^2 + 5m -14
y^2 - 9y + 20
x^2 - 6 - x
x^2 - 9x + 8
c^2 + 5c - 24

IMAGEN:

VÍDEO:

7° CASO : TRINOMIO DE LA FORMA ax^2 + bx + c

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma (a-b)(a+b), uno negativo y otro positivo.

REGLA

Mostrar cómo factorizar trinomios de la forma ax2+bx+c. En el texto de Baldor lo realizan por tanteo. El método dice que lo que tengo que hacer es tratar de convertir la expresión a un trinomio de la forma [(ax)2 + b(ax) + ca ]/2. En el primer ejemplo lo que hicimos es multiplicar toda la expresión inicial por 2, y dividirla por 2 para que no se altere. Esto con el objetivo de dejar un polinomio que se pueda resolver por tanteo. Después de resuelto el trinomio de la forma ax2+bx+c, debemos recordar que todo está dividido sobre un número y realizar la simplificación. En ocasiones puede llegar a suceder que necesitemos sacar factor común para poder realizar fácilmente la simplificación.

EJERCICIOS :

EJERCICIOS SIN RESOLVER :

2x^2 + 3x - 2
3x^2 -5x - 2
6x^2 + 7x + 2
5 x^2 + 13x - 6
6x^2 - 6 - 5x
12x^2 - x - 6
4a^2 + 15a + 9
3 + 11a + 10a^2
12m^2 - 13m -35

IMAGEN:

VÍDEO:

8° CASO : CUBO PERFECTO DE BINOMIOS

REGLA :

Para factorarlo se extrae la raíz cúbica al primer y cuarto términos, con las raíces formamos un binomio; separando las raíces con (+) si todos los términos del cubo son positivos y con ( - ) si los términos del cubo son alternadamente positivos y negativos; el binomio formado se eleva al cubo.

EJERCICIOS :

EJERCICIOS SIN RESOLVER :

a^3 + 3a^2 + 3a + 1
27 - 27x + 9x^2 - x ^3
m^3 + 3m^2n + 3 mn^2 + n^3
1 + 3a^2 - 3a - a^3
8 + 12a^2 + 6a ^4 + a^6
125x^3 + 1 + 75x^2 + 15x
8a^3 - 36a^2b + 54ab^2 + 15x

IMAGEN:

9° CASO : SUMA O DIFERENCIA DE CUBOS PERFECTOS

REGLA

La suma de dos cubos perfectos, es igual a la suma de sus raíces cúbicas, (a+b); multiplicado por el cuadrado de la 1° raíz cúbica, a^2, menos el producto de las dos raíces cúbicas, ab, más el cuadrado de la 2° raíz cúbica, b^2.

EJERCICIOS :

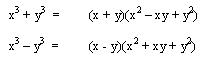
EJERCICIOS SI RESOLVER:

1 + a^3
1 - a^3
x^3 + y^3
m^3 - n^3
a^3 - 1
y^3 + 1
y^3 -1
8x^3 - 1
1 - 8x^3

IMAGEN:

10° CASO : SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES

REGLA:

Organizar los monomios de mayor a menor exponente.
Sacar la raíz n-ésima al primer y segundo término.
Dividir la expresión original entre la suma o resta (de acuerdo al signo del segundo término) de las raíces.
Igualar éste término a la suma de los (n-1) monomios en donde se observa que el primer termino comienza elevado a la (n-1) y termina en 0, mientras que el segundo término comienza en 0 y termina en (n-1).
Pasar a multiplicar el término ubicado en el denominador a la expresión obtenida en el paso anterior.
Verificar que la expresión da el ejercicio que se quiere desarrollar.

EJRCICIOS :